< f a c t o r i a l n ! >

http://factorielle.free.fr/

This site is a reference for the factorial n! notation and tries to propose a more complete documentation to this subject. We hope you'll be satisfied; for any remarks, links, informations, suggestions etc. please don't hesitate to share with us your ideas! We'll be very thankful for that! :)

Page contents:
- Definition
- Some calculations
- History, biographies
- Programming
- Links
- About this site

Definition

In mathematics, the factorial of a natural number n is the product of the positive integers less than or equal to n. This is written as n! and pronounced 'n factorial'.

The factorial function is formally defined by

$n!=\prod_{k=1}^n k\qquad\mbox{for all }n\ge0.$

For example,

5! = 1 * 2 * 3 *4 * 5 = 120

This definition implies in particular that

0! = 1

because the product of no numbers at all is 1. Proper attention to the value of the empty product is important in this case, because

it makes the above recursive relation work for n = 1;
many identities in combinatorics would not work for zero sizes without this definition.

The factorial function can also be defined (for non-integer values of z), via the gamma function:

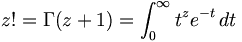
$z!=\Gamma(z+1)=\int_{0}^{\infty} t^z e^{-t}\, dt$

Applications

Factorials are important in combinatorics. For example, there are n! different ways of arranging n distinct objects in a sequence. (The arrangements are called permutations.) And the number of ways one can choose k objects from among a given set of n objects (the number of combinations), is given by the so-called binomial coefficient

${n\choose k}={n!\over k!(n-k)!}.$

Factorials also turn up in calculus. For example, Taylor's theorem expresses a function f(x) as a power series in x, basically because the n-th derivative of xⁿ is n!. Factorials are also used extensively in probability theory.

Calculating factorials

The numeric value of n! can be calculated by repeated multiplication if n is not too large. That is basically what pocket calculators do. The largest factorial that most calculators can handle is 69!, because 70! > 10¹⁰⁰.

When n is large, n! can be estimated quite accurately using Stirling's approximation:

$n!\approx\sqrt{2\pi n}\left(\frac{n}{e}\right)^n.$

Generalizations

The gamma function

The related gamma function Γ(z) is defined for all complex numbers z except for the nonpositive integers (z = 0, −1, −2, −3, ...). It is related to factorials in that it satisfies a recursive relationship similar to that of the factiorial function:

n! = n(n - 1)!

Γ(n + 1) = nΓ(n)

Together with the definition Γ(1) = 1 this yields the equation

$\Gamma(n+1)=n!\qquad\mbox{for all }n\in\mathbb{N},n\ge1.$

Because of this relationship, the gamma function is often thought of as a generalization of the factorial function to the domain of complex numbers. This is justified for the following reasons.

Shared meaning—The canonical definition of the factorial function is the mentioned recursive relationship, shared by both.
Uniqueness—The gamma function is the only function which satisfies the mentioned recursive relationship for the domain of complex numbers and is holomorphic and whose restriction to the positive real axis is log-convex. That is, it is the only function that could possibly be a generalization of the factorial function.
Context—The gamma function is generally used in a context similar to that of the factorials (but, of course, where a more general domain is of interest).

Multifactorials

A common related notation is to use multiple exclamation points to denote a multifactorial, the product of integers in steps of two (n!!), three (n!!!), or more.

n!! denotes the double factorial of n and is defined recursively by

$n!!= \left\{ \begin{matrix} 1,\qquad\quad\ &&\mbox{if }n=0\mbox{ or }n=1; \\ n(n-2)!!&&\mbox{if }n\ge2.\qquad\qquad \end{matrix} \right.$

For example, 8!! = 2 · 4 · 6 · 8 = 384 and 9!! = 1 · 3 · 5 · 7 · 9 = 945. The sequence of double factorials for n = 0, 1, 2,... starts

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, ...

Some identities involving double factorials are:

n! = n!!(n - 1)!!

(2n)!! = 2ⁿn!

$(2n+1)!!={(2n+1)!\over(2n)!!}={(2n+1)!\over2^nn!}$

$\Gamma\left(n+{1\over2}\right)=\sqrt\pi{(2n-1)!!\over2^n}$

One should be careful not to interpret n!! as the factorial of n!, which would be written (n!)! and is a much larger number.

The double factorial is the most commonly used variant, but one can similarly define the triple factorial (n!!!) and so on. In general, the k-th factorial, denoted by n!^(k), is defined recursively as

$n!^{(k)}= \left\{ \begin{matrix} 1,\qquad\qquad\ &&\mbox{if }0\le n<k; \\ n(n-k)!^{(k)},&&\mbox{if }n\ge k.\quad\ \ \, \end{matrix} \right.$

Hyperfactorials

Occasionally the hyperfactorial of n is considered. It is written as H(n) and defined by

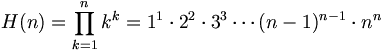
$H(n) =\prod_{k=1}^n k^k =1^1\cdot2^2\cdot3^3\cdots(n-1)^{n-1}\cdot n^n$

For n = 1, 2, 3, 4,... the values of H(n) are 1, 4, 108, 27648,...

The hyperfactorial function is similar to the factorial, but produces larger numbers. The rate of growth of this function, however, is not much larger than a regular factorial.

Superfactorials

The superfactorial of n, written as n$ (the $ should really be a factorial sign ! with an S superimposed) has been defined as

n$ = n⁽⁴⁾n

where the ⁽⁴⁾ notation denotes the hyper4 operator, or using Knuth's up-arrow notation.

$n$=(n!)\uparrow\uparrow(n!)$

The sequence of superfactorials starts:

1$ = 1

2$ = 2² = 4

$3$=6\uparrow\uparrow6=6^{6^{6^{6^{6^6}}}}$

A lot of formulas and examples are on the examples page.

Some calculations

0!		10! .. 500!	666!
1000!	2000!	5000!	2002!
10 000!	20 000!	50 000!	2003!
100 000!	200 000!	500 000!	150 000!
1 000 000!	2 000 000!

Download this calculations in compressed.tar.bz2 files.

History, biographies

Multiple scientists worked on this subject, but the principal inventors are J. Stirling in 1730 who gives the asymptotic formula after some work in collaboration with De Moivre, then Euler in 1751 and finally C. Kramp and Arbogast who introduces between 1808 and 1816 the actual notation: n!. Of course other scientists such as Taylor also worked a lot with this notation.

Computer programming

Factorial can be calculate with recursive or iterative algorithms. Some programs to calculate n!:

Ada
fact.adb
Calculate et give n! for 0 <= n <= 12.

80*86 assembler
fact.asm

C language
fact_c.tar.gz
By Julien Graziano.

C++
fact.cpp
By Calum Grant.

Haskell
Evolution of a haskell programmer
By Fritz Ruehr.

Java
Fact.java
Calculate and give n! for 0 <= n <= 12.

Perl
fact1.pl
fact2.pl

PHP
fact.php
By Pierre.

Python
fact.py

Scheme
fact.scm
Calculate and give n! for n! < 2^32.

UNIX Shell
fact.sh
Calculate and give n! pour 0 <= n <= 12.

Links

http://regentsprep.org/Regentspics/factnot/Lfact.htm <-- Oswego City School (State University of New York) District Regents Exam Center. For young people, the factorials explained with many animations. A lot of other ressources for mathematics.
http://members.aol.com/jeff570/mathsym.html<-- Earliest Uses of Various Mathematical Symbols, site presenting the origin of other usual mathematical notations, + - / etc. Florida, USA.
http://mathworld.wolfram.com/Factorial.html
http://www.fact-index.com/f/fa/factorial.html
http://astronomy.swin.edu.au/~pbourke/analysis/gammafcn/
http://encyclopedia.thefreedictionary.com/factorial
http://www.yourencyclopedia.net/Factorial.html
http://www.luschny.de/math/factorial/FastFactorialFunctions.htm <-- this site shows some intresting algorithmic ways to compute the factorial

About this site

Why this site?

We didn't find any site dedicated to this notation. Then we decided to put online our works about n!, made in computer science and in the epistemological option "histoire du concept du nombre" (number's concept history), at the University of Sciences and Technologies of Lille. Then we never stop to work on it. Because we support the share of knowledge, we put a lot of parts of this site into Wikipedia, so they can be frequently improved.

latest updates
statistics

Authors:

Jiel Beaumadier | mail
Matěj Hausenblas | mail
Matěj et Jiel are both active in free software community, they contribute to some organizations such as Campux and Léa-Linux.

Contributions:
Pierre, Andrei Didorenko, Julien Graziano

Special thanks to:
Eliane Cousquer
Jean-Christophe Routier
Marie-Hélène Verrons
Eric Wegrzynowski

Page contents